Answer for HW1

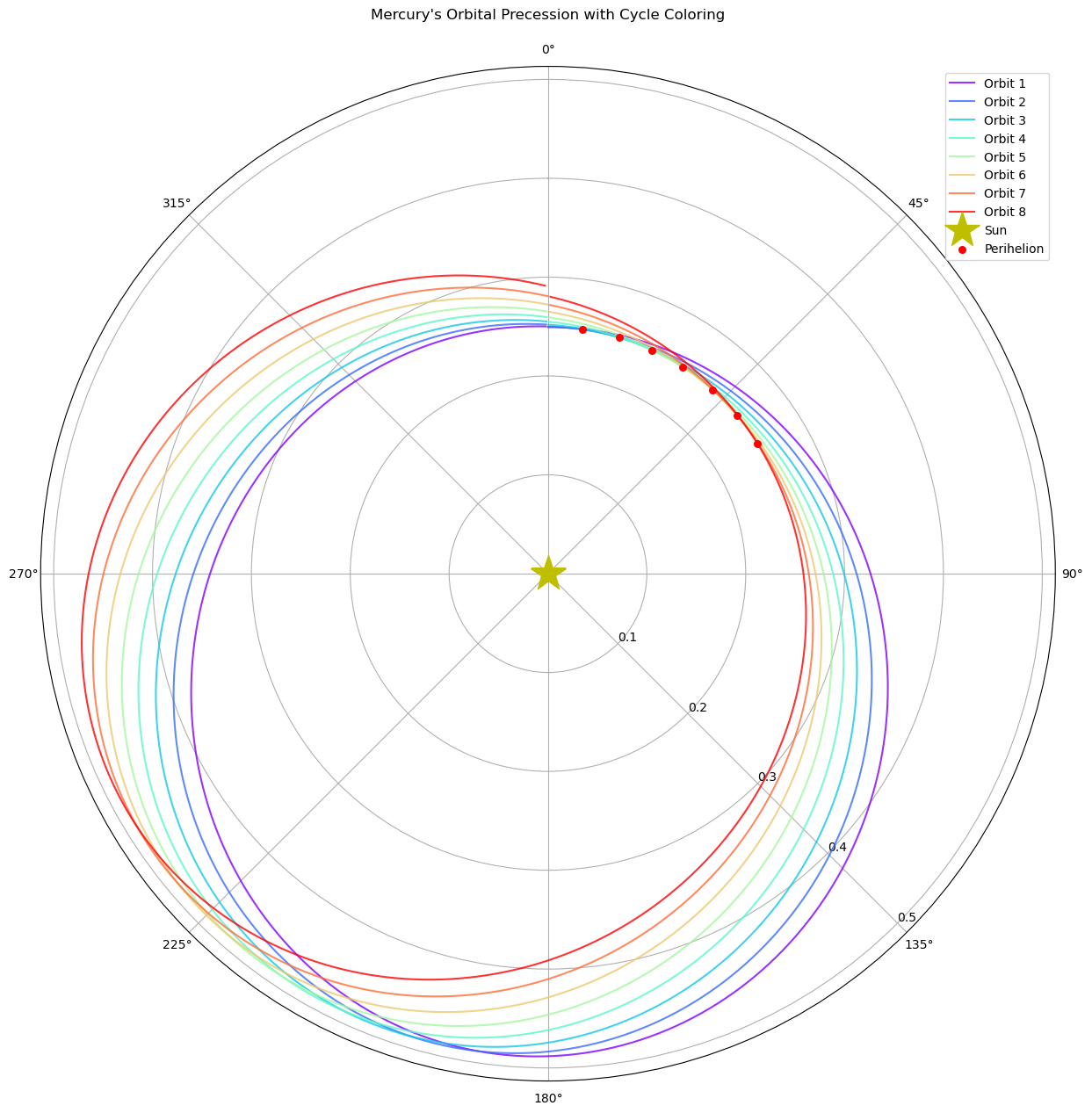
1 球坐标

1.1

首先注意到，球坐标系 $(r, θ, ϕ)$ 与直角坐标系 $(x, y, z)$ 的转换关系为：

{\begin{aligned} x & = r \sin θ \cos ϕ \\ y & = r \sin θ \sin ϕ \\ z & = r \cos θ \end{aligned}

对应的三个正交单位矢量为：

{\begin{aligned} {\hat{e}}_{r} & = \frac{\partial \vec{r}}{\partial r} = \sin θ \cos ϕ \hat{i} + \sin θ \sin ϕ \hat{j} + \cos θ \hat{k} \\ {\hat{e}}_{θ} & = \frac{1}{r} \frac{\partial \vec{r}}{\partial θ} = \cos θ \cos ϕ \hat{i} + \cos θ \sin ϕ \hat{j} - \sin θ \hat{k} \\ {\hat{e}}_{ϕ} & = \frac{1}{r \sin θ} \frac{\partial \vec{r}}{\partial ϕ} = - \sin ϕ \hat{i} + \cos ϕ \hat{j} \end{aligned}

利用链式法则，可以求得三个单位矢量对时间的变化率：

{\begin{aligned} {\dot{\hat{e}}}_{r} & = \dot{θ} {\hat{e}}_{θ} + \dot{ϕ} \sin θ {\hat{e}}_{ϕ} \\ {\dot{\hat{e}}}_{θ} & = - \dot{θ} {\hat{e}}_{r} + \dot{ϕ} \cos θ {\hat{e}}_{ϕ} \\ {\dot{\hat{e}}}_{ϕ} & = - (\sin θ {\hat{e}}_{r} + \cos θ {\hat{e}}_{θ}) \dot{ϕ} \end{aligned}

1.2 速度表达式

位置矢量 $\vec{r} = r {\hat{e}}_{r}$ 对时间求导，得到速度矢量：

\vec{v} = \dot{\vec{r}} = \dot{r} {\hat{e}}_{r} + r {\dot{\hat{e}}}_{r} = \dot{r} {\hat{e}}_{r} + r \dot{θ} {\hat{e}}_{θ} + r \dot{ϕ} \sin θ {\hat{e}}_{ϕ}

1.3 加速度表达式

速度矢量 $\vec{v}$ 再次对时间求导，得到加速度矢量：

\vec{a} = \dot{\vec{v}} = (\ddot{r} - r {\dot{θ}}^{2} - r {\dot{ϕ}}^{2} \sin^{2} θ) {\hat{e}}_{r} + (r \ddot{θ} + 2 \dot{r} \dot{θ} - r {\dot{ϕ}}^{2} \sin θ \cos θ) {\hat{e}}_{θ} + (r \ddot{ϕ} \sin θ + 2 \dot{r} \dot{ϕ} \sin θ + 2 r \dot{ϕ} \dot{θ} \cos θ) {\hat{e}}_{ϕ}

2 开普勒运动常数

这一题可参阅讲义。结果是：

\frac{d v}{d θ} = \frac{G M}{L}

其中，M 是中心天体质量，L 是运动天体的(单位质量)角动量。

3 双曲线轨道

3.1

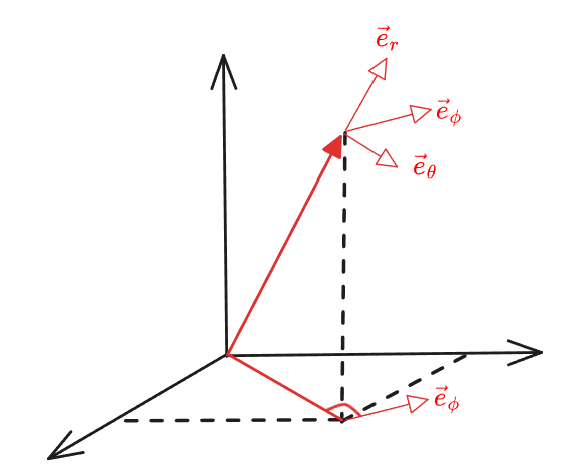
如图，构造步骤：

给定一个圆，圆心 $F_{1}$ ，半径 $R$ ；取圆外一点 $F_{2} $ 。
在圆上取动点 $P$ ，作 $P F_{2}$ 的中垂线，与 $P F_{1}$ （延长线）交于点 $Q$ 。
动点 $P$ 运动时，点 $Q$ 的轨迹即为以 $F_{1} $ 、 $F_{2} $ 为焦点的双曲线。（因为 $P Q = Q F_{2}$ ，所以 $| Q F_{2} - Q F_{1} | = | P F_{1} | \equiv R$ ）

Tip

和椭圆轨道一样，这里的中垂线也是双曲线轨道在 Q 点的切线。

3.2

因为角动量守恒依旧成立，所以第二问的结论依旧是可用的，于是 $Δ v \propto Δ θ$ ，得到的速度图仍然是一个圆（左图）。

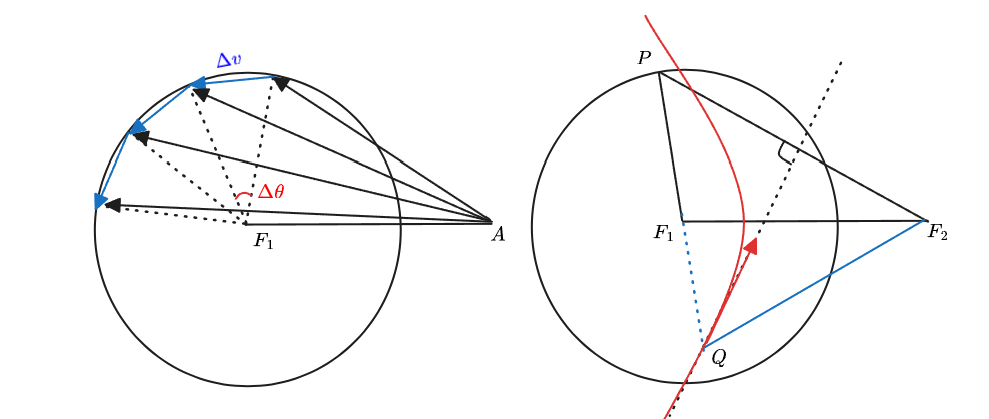
将速度图旋转 90 度，方向与中垂线平行，同时也是双曲线的切线。随着 $θ$ 变化，将得到的一系列切线连接，就得到轨道为双曲线。

更严格一点来说

记 $A F_{1} = C$ ，速度圆半径为 $R$ ，那么根据速度圆，可以假设：

\vec{v} = [\begin{matrix} v_{x} \\ v_{y} \end{matrix}] = [\begin{matrix} - R \sin θ \\ R \cos θ + C \end{matrix}]

将坐标系旋转到极坐标，得到：

\vec{v} = [\begin{matrix} v_{r} \\ v_{θ} \end{matrix}] = [\begin{matrix} \dot{r} \\ r \dot{θ} \end{matrix}] = [\begin{matrix} \cos θ & \sin θ \\ - \sin θ & \cos θ \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \end{matrix}] = [\begin{matrix} - C \sin θ \\ C \cos θ + R \end{matrix}]

得到：

\frac{d r}{d θ} = \frac{d r / d t}{d θ / d t} = r \frac{\dot{r}}{r \dot{θ}} = r \frac{C \sin θ}{R + C \cos θ}

这个方程容易通过分离 $r$ 和 $θ$ 来求解，最后的到其满足圆锥曲线方程 $r = \frac{p}{1 + e \cos θ}$ ，其中 $e = \frac{C}{R}$ ，p 是积分常数，也就是说

C < R 时，也就是 A 点在圆内时，e<1，对应椭圆；
圆、双曲线、抛物线完全类似。

3.3

此时，金原子核可视为固定不变，而库仑力和万有引力均为平方反比力，性质相似，所以上述讨论也成立， $α$ 粒子轨迹为双曲线，原子核位于 $F_{2}$ 。

4 进动

4.1

根据广义相对论修正 $F^{(G R)} = - \frac{3 (G M)^{2} p}{r^{4} c^{2}}$ , 行星在公转一周后，位矢和速度方向都会发生偏转，这个偏转就是每运行轨道一圈的进动角，记为 $Δ$ 。题目缺少一个说明：广义相对论修正力 $F^{(G R)}$ 的方向和牛顿万有引力一致，加上这个说明，就得到：

\frac{Δ}{2 π} = \frac{δ Δ v}{Δ v} = \frac{F^{(G R)}}{F^{(N e w t o n)}} = \frac{3 (G M)^{2} p}{r^{4} c^{2}} / \frac{G M}{r^{2}} = \frac{3 G M p}{r^{2} c^{2}}

$δ Δ v$ 是在每个微小速度变化 $Δ v$ 时，广义相对论修正带来的进动。在离心率 $e$ 较小时， $p \approx a, r \approx a$ ，于是：

Δ \approx \frac{6 π G M}{a c^{2}}

4.2

将题目所给数据带入上式，得到：

Δ \approx \frac{6 π}{5.8 \times 10^{7} k m} \times 1.5 k m \approx 4.9 \times 10^{- 7} r a d

Info

hw1作业答案到此结束。如果感兴趣，可以往后阅读。

Appendix 稍微严格一点的水星进动计算过程%

一般描述单位质量天体的运动的比耐公式是这样的：

\vec{F} = - h^{2} μ^{2} (\frac{d^{2} μ}{d φ^{2}} + μ) \vec{e_{r}}, μ = \frac{1}{r}

已知 $F^{(G R)} = - \frac{3 (G M)^{2} p}{r^{4} c^{2}}$ ，而 $h = \sqrt{G M p} $ 是单位质量的角动量，得到：

\vec{F} = {\vec{F}}^{(N e w t o n)} + {\vec{F}}^{(G R)} = - G \frac{M}{r^{2}} (1 + \frac{3 h^{2}}{r^{2} c^{2}}) \vec{e_{r}}

使用变量替换 $u = \frac{G M}{r}$ ，可以得到：

\frac{d^{2} u}{d^{2} φ} + u = \frac{G^{2} M^{2}}{h^{2}} + \frac{3 u^{2}}{c^{2}}

上式的红色项正是广义相对论所带来的一阶修正。去掉该项，就是在力学中学过的、求解开普勒运动所得到的方程，我们可以发现解为 $r = \frac{h^{2} / G M}{1 + e \cos φ}$ ，这正是圆锥曲线。现在我们好奇，引入的项显然是一个小量，会让原轨道偏离圆锥曲线，这个偏离的曲线是什么形状？

这个方程是非线性的，不便于解析处理，考虑到 $r ≫ r_{g} = \frac{2 G M}{c^{2}}$ ，可以求其微扰解，也就是直接将零阶解 $r = \frac{h^{2} / G M}{1 + e \cos φ}$ 带入方程，注意到 $u^{2} \approx \frac{1 + 2 e \cos φ}{h^{4} / G^{4} M^{4}}$ ，取 $e ≪ 1$ （尽管对于水星 $e = 0.2056$ 不算特别小，但近似仍是有效的），得到：

\frac{d^{2} u}{d^{2} φ} + u = \frac{G^{2} M^{2}}{h^{2}} + 3 \frac{G^{4} M^{4}}{h^{4} c^{2}} (1 + 2 e \cos φ)

右侧第一项 $\frac{G^{2} M^{2}}{h^{2}}$ 是带有初始位移的简谐振动项，对应的正是零阶解（轨道为圆锥曲线）；后两项虽然都带有高阶小量 $\frac{G^{4} M^{4}}{h^{4} c^{2}}$ ，但由于 $\cos φ$ 是共振项(回忆力学的受迫振动：共振)，因此括号两项当中只有 $2 e \cos φ$ 项被保留，得到的解是圆锥曲线+共振：

u = \frac{G^{2} M^{2}}{h^{2}} [1 + e \cos φ + 3 {(\frac{G M}{h c})}^{2} e φ \sin φ] \approx \frac{G^{2} M^{2}}{h^{2}} [1 + e \cos (1 - 3 {(\frac{G M}{h c})}^{2}) φ]

可见当水星运行 $Δ φ$ 时，相对于零阶解，新轨道的相位会超前：

\frac{Δ φ}{1 - 3 {(\frac{G M}{h c})}^{2}} - Δ φ \approx 3 {(\frac{G M}{h c})}^{2} Δ φ

取一周 $Δ φ = 2 π$ 得到近地点在公转一周后的进动角度：

Δ = 6 π {(\frac{G M}{h c})}^{2} \approx {0.1034}^{″} \approx 5.014 \times 10^{- 7} r a d

它给出的结果是 $Δ \approx {43.03}^{″} / c e n t u r y$ ，幸好对水星的观测能一直追溯到 1765 年，Clemence 在 1943 年分析了这些数据，得出 $Δ = 43.11 \pm {0.45}^{″} / c e n t u r y$ ，证实了这一预言。